Characterization of the Performance of Robot Localization
| Motivation |
The goal of this work is to provide theoretical tools for characterizing the
accuracy attainable during robot localization. In particular, our work focuses
on four classes of localization problems:
1. Cooperative Localization (CL)
2. Simultaneous Localization and Mapping (SLAM)
3. Cooperative SLAM (C-SLAM)
4. Cooperative Localization and Target Tracking (CLATT)
All these areas have been very active topics of research in recent years. However, most of the research has focused on implementation techniques, as well as on addressing the problem of computational complexity. The issue of analytical evaluation of performance has been largely ignored in the literature, with only few exceptions of limited scope. As a result, questions such as "How much more accurate will the position estimates become if the odometry noise variance is reduced by 50%?", or "Will my robot with its current sensors achieve localization errors smaller than 1m after 1h of operation?" can only be answered after extensive simulations and/or time-consuming experimentation. Clearly, this is a significant obstacle for robot design. Our work aims at providing analytical means for addressing similar questions.
| Contribution |
T
he primary contribution of this work is the derivation of theoretical tools for evaluating the performance, in terms of positioning accuracy, of CL, SLAM, and C-SLAM. In particular, we present analytical expressions that determine the guaranteed accuracy of localization, as closed-form functions of the following system design parameters:the accuracy of the robots' sensors
the number of robots and features
the structure of Relative Position Measurement Graph (RPMG) that describes the measurement topology between the robots and/or landmarks
the statistical properties of the robots' trajectories
the spatial distribution of features, in SLAM and C-SLAM
The derivation of analytical expressions enables predicting the localization accuracy that a given robot design will attain in an application. This facilitates the process of selecting the appropriate sensors necessary to achieve the accuracy requirements of a given task. Moreover, availability of closed-form results enables the study of the properties of positioning errors during CL, SLAM, and C-SLAM. This helps develop an intuitive understanding of the interactions between system parameters, and leads to design rules, which reduce the time and effort required for new robot designs .Today, experimentation and numerical simulations are the only tools available for studying the tradeoffs between selections of such parameters. As a result, the effort and cost necessary for robot design are increased.
| Approach |
Our specific goal is to study the properties of the state covariance matrix during pose estimation, since this matrix is a concrete measure of the uncertainty. This problem is challenging, since the models describing both the motion and the measurements of robots moving in 2D and 3D are generally nonlinear. As a result, the Extended Kalman Filter (EKF), rather than the linear Kalman filter, is applied for state estimation, and the Riccati recursion, which describes the time evolution of the covariance, is time-varying. For this Riccati no closed-form solution exists in the general case.
Therefore, in order to analytically study the properties of CL for robots moving in 2D, we resort to the derivation of upper bounds for the covariance of the position estimates. In particular, in our work we derive upper bounds on
the worst-case uncertainty of the position estimates, and
the expected uncertainty of the position estimates
These bounds are closed-form functions of the system parameters mentioned above, and enable a detailed study of the effect of any design choice on the position accuracy.
| Results |
We have carried out extensive simulation tests and real-world experiments to validate the theoretical analysis, and to demonstrate its usefulness in predicting the performance of localization systems. In what follows, some representative results from CL and SLAM are described:
A. Cooperative Localization
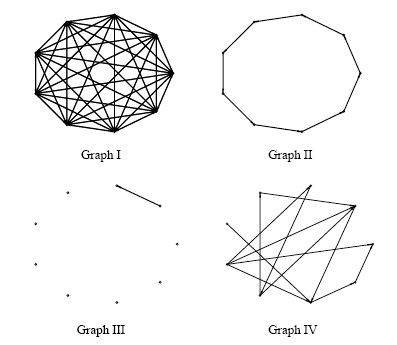
One of the primary uses of the derived closed-form expressions, is for the study of the properties of the localization accuracy. We here present simulation results showing the effects of RPMG reconfigurations. The behavior of the covariance that is observed in the plots is predicted by, and corroborates, the theoretical analysis. The following figure shows the four different RPMG topologies that are used for this simulation test:

Figure 1
For this simulation, a homogeneous robot team comprising 9 robots is considered. The time-evolution of the covariance is shown in Figure 2:
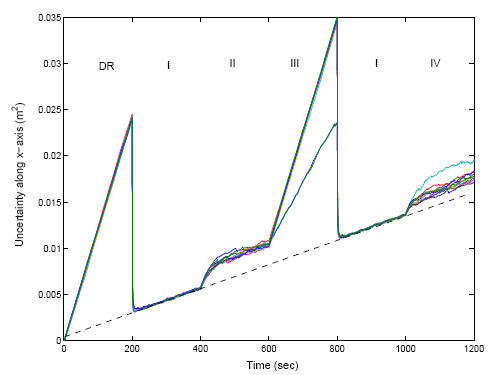
Figure 2
In this plot, the covariance along the x axis for all robots is plotted. During the first 200sec of their mission, the robots localize independently (Dead Reckoning, DR). At t = 200sec, the robots start recording relative position measurements, which are described by a complete RPMG topology (cf. Fig. 1-I). The sharp improvement in localization accuracy, as well as the decrease in the rate of covariance increase, becomes evident. At t = 400sec, the RPMG topology changes to a sparser, ring graph (cf. Fig. 1-II). Clearly, after an initial transient response, the rate at which the covariance increases with the new RPMG topology remains unchanged, and a small constant penalty in performance is incurred. This result, which has very important practical implications, is predicted and explained by our theoretical analysis.
At t = 600sec, a simulated communication failure occurs, and only two of the robots are able to record and communicate relative position measurements (cf. Fig. 1-III). Careful examination of the plot reveals that the rate of uncertainty increase for these two robots is precisely half that of the rest of the robots, which localize independently. This result verifies an important prediction of our analysis, which stipulates that the rate of uncertainty increase, for homogeneous robot teams, is inversely proportional to the number of robots.
At t = 800sec, the initial complete graph topology is restored (cf. Fig. 1-I). We observe that, as expected by the theoretical analysis, the covariance for all robots is identical to the one that would arise if no RPMG reconfigurations had occurred. Finally, at t = 1000sec, the RPMG assumes a random (i.e., non-canonical) topology (cf. Fig. 1-IV). Clearly, for this topology the asymptotic rate of uncertainty increase for all robots is identical, even though the constant term of the covariance varies among robots.
B. Simultaneous Localization and Mapping
For the case of SLAM, we present experimental results that demonstrate the usefulness of the analytical covariance bounds for predicting the accuracy of the robot's and landmarks' localization. In this experiment, a Pioneer 3 robot equipped with two opposite-facing SICK LMS200 laser scanners, which provide a 360o field of view, was employed. The robot is shown in Fig. 5:

Figure 5
During the experiment, the robot moves randomly while performing SLAM in an area
of approximate dimensions 10m◊4m. The laser scans are processed for detecting
four prominent corners in the area, which are used as landmarks. For detecting
each corner, line-fitting is employed to compute the equations of adjacent wall
lines, and the intersection of these lines is determined. The robot also
receives translational and rotational velocity measurements from its wheel
encoders. The estimated robot trajectory, as well as the landmark positions, are
shown in Fig. 6. In the same figure, a sample laser scan is superimposed (after
being transformed to the global frame), to illustrate the geometry of the area
where the robot operates.
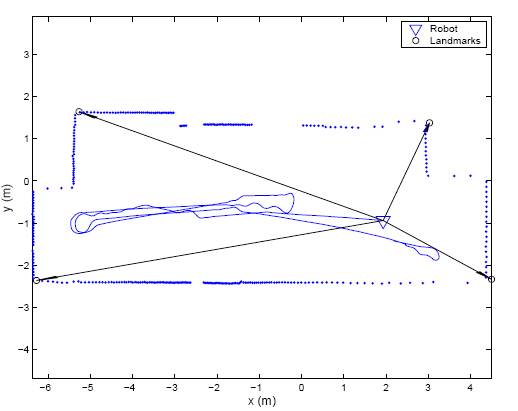
Figure 6
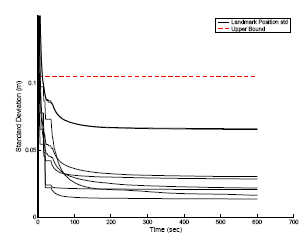
In Fig. 7, the standard deviation of the estimation errors (solid lines), as
this is computed by the filter, is compared to the standard deviation computed
with the theoretically derived
bounds (dashed lines).
(a)
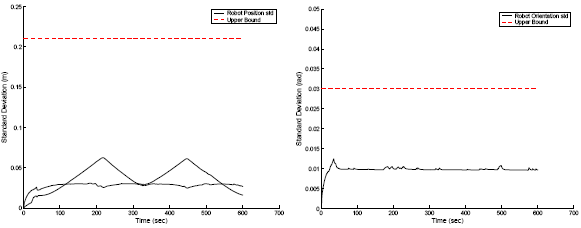
(b) (c)
|
Figure 7: (a) the landmarksí position standard deviation and corresponding upper bound (b) The robotís position standard deviation and corresponding upper bound (c) The robotís orientation standard deviation and corresponding upper bound. |
These plots demonstrate that the derived analytical bounds can be employed in order to predict the localization accuracy of localization, without having to resort to extensive simulations, or experimentation. This can significantly reduce the time and cost needed for experimentation during the design of a robot system.
| Related Publications |
1. A.I. Mourikis, S.I. Roumeliotis: "Predicting the Performance of Cooperative Simultaneous Localization and Mapping (C-SLAM),'' International Journal of Robotics Research 25(12), pp. 1273-1286, Dec 2006.
2. A.I. Mourikis, S.I. Roumeliotis: "Performance Analysis of
Multirobot Cooperative Localization,'' IEEE Transactions on Robotics
22(4), pp. 666-681, Aug. 2006.
3. F.M. Mirzaei, A.I. Mourikis, S.I. Roumeliotis: "On the Performance of Multi-robot Target Tracking," Proceedings of the IEEE International Conference on Robotics and Automation, April 10-14 2007, Rome, Italy, pp. 3482-3489.
4.
A.I. Mourikis, S.I. Roumeliotis: "Analytical Characterization of the Accuracy of SLAM without Absolute Orientation Measurements," Proceedings of Robotics: Science and Systems, Philadelphia, PA, Aug. 16-19, 2006.
5
. A.I. Mourikis, S.I. Roumeliotis: "Performance Bounds for Cooperative Simultaneous Localization and Mapping (C-SLAM)," Proceedings of Robotics: Science and Systems, June 8-11, 2005, Boston, MA, pp. 73-80.
6. A.I. Mourikis, S.I. Roumeliotis: "Analysis of Positioning Uncertainty in Simultaneous Localization and Mapping (SLAM)," in Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, September 28 - October 2, 2004, Sendai, Japan, pp. 13-20.
7
. A.I. Mourikis, S.I. Roumeliotis: "Analysis of Positioning Uncertainty in Reconfigurable Networks of Heterogeneous Mobile Robots,'' in Proceedings of the IEEE International Conference on Robotics and Automation, April 26-May 1, 2004, New Orleans, LA, pp. 572-579.
| Acknowledgements |
This work was supported by the University of Minnesota (GiA Award, DTC), the Jet Propulsion Laboratory (Grant No. 1248696, 1251073), the NASA Mars Technology Program (MTP-1263201), and the National Science Foundation (EIA-0324864, IIS-0643680).